Hello, friends today I am going to discuss the "moment of force" in which you will be aware of all aspects related to the moment of force such as their classification, principle, geometrical representation, application, etc.
So without wasting time let's get started.
What is a Moment of Force?
The tendency of forces is not only to move a body but also to rotate the body.
This rotational tendency of a force is called a moment or moment of force.
Mathematically It can be defined as " The product of force and perpendicular distance from the point to the line of action of the force is called the moment of a force about that point".
It can be denoted by M.
So,
The formula of moment of force can be written as,
M = F × d
Where,
M = Moment
F = Force
d = Perpendicular Distance
The SI unit of the moment of force is newton meter (N-m) while in CGS it can be written as newton centimeter (N-cm).
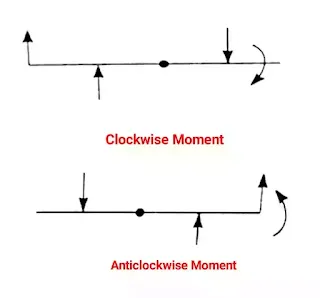
Direction of Moment
According to the direction of the moment, it is divided into two types.
- Clockwise Moment
- Anticlockwise Moment
Clockwise Moment
If a force acting on a body has the tendency to rotate the body in a clockwise direction, then the moment produced is called a clockwise moment.
Anticlockwise Moment
If a force acting on a body has the tendency to rotate the body in an anticlockwise direction, then the moment so produced is called an anticlockwise moment.
Classification of Moment of Force
There are the following classifications of Moment:
- Turning Moment
- Bending Moment
- Twisting Moment
Turning Moment
This moment tends to rotate a body about a fulcrum. In this case, the body is free to rotate about a fulcrum.
Bending Moment
This moment tends to bend a body about one of its fixed ends.
Twisting Moment
This moment twisted a shaft about one of its fixed ends.
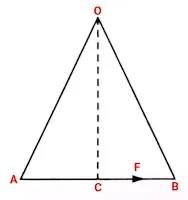
Geometric Representation of Moment of Force
The moment of a force about a point is equal to twice the area of the triangle so formed by taking the point as the vertex of the triangle and the line as the base of the triangle.
Let us consider a force F acting on a body and is represented by vector AB.
Let O be the point about which moment of the force is to be calculated.
Then,
Moment of the force about O, M =Fx OC
Moment of the force about O, M = AB x OC
(Clearly seen in figure F = AB)
Now multiplied and divide by 2
Then,
M = 2 x 1/2 AB x OC
As we know,
Area of triangle = 1/2 × base × height
So,
M = 2 x Area of △OAB
Principle of Moment of Force
If a body is in equilibrium under the action of a number of forces acting simultaneously on a body, then the algebraic sum of moments of all the forces about a point, in their plane is zero".
or
If a body is in equilibrium under the action of a number of forces acting simultaneously on the body, then the algebraic sum of the clockwise moments of the forces about a point is equal to the sum of anticlockwise moments of the forces about the same point."
That means the algebraic sum of all the moments must be zero.
ΣM = 0
Let us consider four coplanar forces F1, F2, F3, and F4, acting on a body while the body is in equilibrium.
Let O be the point about which body can rotate. Let d1, d2, d3, and d4, be the perpendicular distance of the point O from the line of action of the forces F1, F2, F3, and F4, respectively.
Then,
Moment of force F1 = F1 x d1 (Anticlockwise)
Moment of force F2 = F2 x d2 (Anticlockwise)
Moment of force F3 = F3 x d3 (Clockwise)
Moment of force F4= F4 x d4 (Clockwise)
The resultant moment
ΣM = F1 x d1 + F2 x d2 - F3 x d3 - F4 x d4
According to the principle of the moment of force, the algebraic sum of all the moments must be zero.
So,
ΣM = 0
F1 x d1 + F2 x d2 - F3 x d3 - F4 x d4 =0
F1 x d1 + F2 x d2 = F3 x d3 + F4 x d4
Sum of Anticlockwise moments = Sum of clockwise moments
This verifies the principle of moments of force.
Applications of Moments of Force
Moments of force have many engineering applications such as it is used in levers, common steel yards, lever safety valves, etc.
Related Articles:
.Law of Parallelogram of Forces
So here I discussed what is a moment of force is? Classification of the moment, the principle of a moment of force as well as application of moment of force.
I hope you all enjoy these topics.
Thank You.






2 Comments