In this article, you will learn a complete overview of the modulus of resilience such as its definition, formula, and unit, and the last also calculates the modulus of resilience related numerical problems.
But before knowing the modulus of resilience first we need to know about resilience, proof resilience, strain energy, etc.
So, let’s know about each of the aspects related to the modulus of resilience in detail.
Strain Energy
Energy is stored due to Strain.
When work is done on specimens, this work converts into the energy of specimens. Since this energy is created due to strain, it is called strain energy.
It is denoted by the U.
U = 1/2(σ × ε × V)
Where,
U = Strain Energy
ε = Strain
V = Volume Of the Body
σ = Stress
What is Resilience?
Resilience is basically the energy stored by material within the elastic limit.
U = (σ² × V)/2E
Where,
U = Strain Energy
σ = Stress
E = Young's Modulus
V = Volume Of Body
Proof Resilience
The Maximum energy stored at the Elastic limit is called Proof Resilience.
Modulus of Resilience
It is defined as the Proof resilience per unit volume.
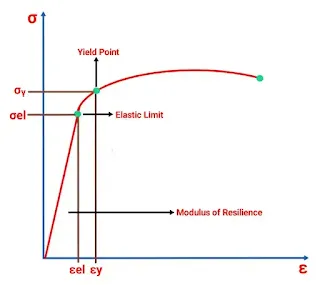
In addition to providing strength values for a material, the stress-strain diagram provides insight into the energy-absorbing characteristics of a material.
This is because the stress-strain diagram involves both loads and deflections, which are directly related to energy.
The capacity of a material to absorb energy within its elastic range is called resilience which has already been discussed above.
The modulus of resilience of a material is defined as the energy absorbed per unit volume without permanent deformation and is equal to the area under the stress-strain curve up to the elastic limit.
The elastic limit is often approximated by the yield point since it is more readily determined given,
Ur = ∫ (σ × dE)
From 0 to σᵧ.
Where σᵧ, is the stress at the yield point.
If the stress - strain is linear to the yield point, then the area under the curve is simply a triangular area ;
Thus,
Ur = 1/2 (σᵧ × εᵧ)
As we know,
ε = σ/E
So,
Ur = 1/2 (σᵧ × σᵧ/E)
Ur = 1/2 (σ²ᵧ/E)
Where,
Ur = Modulus of resilience
σᵧ = Stress up to yield point
E = Young's Modulus
This relationship indicates that for two materials with the same yield strength.
The less stiff material ( lower E ), will have greater resilience, that is, an ability to absorb more energy without yielding.
Then,
Its value is
Ur = σ²/2E
Where,
Ur = Modulus of resilience
σ = Stress
E = Young's Modulus
ε = Strain
Unit of Modulus of Resilience
SI System
As we know in the SI system, the unit of proof resilience is joule and the unit of volume is in m³.
So,
As we know,
Modulus of Resilience =
Proof resilience/Volume
So the unit of the Modulus of Resilience will be in the SI system,
Joule/m³
FPS System
As we know in the FPS system, the unit of proof resilience is in Btu (British thermal unit) and the unit of volume is in ft³ (Foot or Feet).
So the unit of the Modulus of Resilience will be in the FPS system,
Btu/ft³
Calculation of Modulus of Resilience
Question
Calculate the modulus of Resilience for steel up to yield stress of 2.5 × 10⁸ N/m² and Young's modulus is 2 × 10¹¹ N/m²?
Given Data,
σ = 2.5 × 10⁸ N/m²
E = 2 × 10¹¹ N/m²
As we know Modulus of Resilience,
Ur = σ²/2E
So, putting these value
(2.5 × 10⁸)²/( 2 × 2 × 10¹¹)
After solving these values the modulus of resilience will obtain.
1.5625 × 10⁵ J/m³
Related Article:
So here you have to know all aspects related to the modulus of resilience. If you have any doubt then you are free to ask me by mail or on the contact us page.
Thank You.



0 Comments