Modulus of Elasticity | Young’s Modulus: Define,Use,Calculus

In this article, you will learn a complete overview of the modulus of elasticity or young’s modulus such as its definition, formula, unit, derivation, application, calculation, and many more. 

Modulus of elasticity or young's modulus is one of the types of elastic constant.

Elastic constants are those constants that determine the deformation produced by a given stress system acting on any material.

The elastic constant measures the elasticity of the material.

It is used to derive the relationship between stress and strain.

For a homogeneous and isotropic material, there are four types of elastic constants:

1. Modulus of Elasticity  or Young’s modulus
2. Modulus of rigidity or Shear modulus
3. Bulk modulus
4. Poisson’s Ratio

Here we only discussed the modulus of elasticity or young's modulus.

So without wasting time let's get started.

What is Modulus of Elasticity or Young's Modulus?

The modulus of elasticity or young's modulus measures the resistance of a material to elastically deform when a force is applied to a material.  

That means A hard material will have a high modulus of elasticity and flexible material will have a low modulus of elasticity.

For example, the modulus of elasticity of steel is about 200 GPa, and the modulus of elasticity of aluminum is 70 GPa.

This simply translates as aluminum is 3 times more flexible than steel.

It is also called Young's modulus or elastic modulus.

Stresses and strains are assumed to be related by Hooke's Law. 

In its simplest form, Hooke's Law can be stated as: In an elastic member, stress is directly proportional to the strain within the elastic limit.

So, Mathematically

σ ∝ ε

σ = E × ε

Where E is a constant which is known as the modulus of elasticity or Young's modulus.

So,

E = σ/ε

Where,

σ = Stress

ε = Strain

E = Modulus of Elasticity

So, the modulus of elasticity can be defined as, 

The ratio of normal stress to the longitudinal strain within the elastic limit is known as the modulus of elasticity or young's modulus.

 

Modulus of Elasticity or Young's Modulus Formula

Consider a Wire AB of length I and radius r  to which normal force f is applied to increase its length to Δl.

So,

As we know, Longitudinal Strain 

Change in Length/Original Length

So,

ε = Δl/l

As we know,

Stress = Force/A

So,

σ = F/A

So,

E = σ/ε

E = (F/A)/(Δl/l)

So,

E = (F × l)/(Δl × A)

Units of Modulus of Elasticity or Young's Modulus

SI Unit

As we know the unit of stress in the SI system is N/m² and the unit of strain is unitless.

So,

Modulus of Elasticity = Stress/Strain

                                    

                                      =  N/m²

Hence in the  SI system, the unit of the modulus of elasticity will be N/m² or Pascal.

FPS Unit

As we know the unit of stress in the FPS system is lb/ft² and the unit of strain is unit less.

So,

Modulus of Elasticity = Stress/Strain

                                      

                                      =  lb/ft²

Hence in the FPS system, the unit of the modulus of elasticity will be lb/ft².

Modulus of Elasticity Dimensional Formula

As we know,

E = σ/ε

Since,

Stress = Force/Area

As we know,

Force = mass (m) × acceleration (a)

So,

Stress = {mass (m) × acceleration (a)}/A

As we know the unit of mass is kg, the unit of acceleration is m/s² and the unit of area is m².

So,

σ = kg × m s ⁻²/m²

 

σ = kg × s ⁻²/m

σ = ML⁻¹T⁻²

Since the strain is unit less quantity so the modulus of elasticity dimensional formula will be:

E = ML⁻¹T⁻²

Application of Modulus of Elasticity

There are many applications of modulus of elasticity which are as follows:

1. The value of the modulus of elasticity is pretty important in the case of deflection of different materials which is used in building and bridge construction.
2. Modulus of elasticity or Young's modulus measures the stiffness and flexibility of the material
3. Modulus of elasticity also defines the relationship between stress and strain in a material.
4. It specifies the material by how much it can extend or shorten under tension or compression respectively.

Now we will know the relation of the modulus of elasticity or Young's modulus with other elastic constants.

So, before knowing let's discuss some introduction to other elastic constants.

Bulk Modulus

It is defined as the ratio of Normal stress to the volumetric strain, within the elastic limit.

It is denoted by K.

Modulus of Rigidity or Shear Modulus

It is defined as the ratio of tangential stress to the shearing strain.

It is denoted by G.

Poisson's Ratio

If a body is stressed within its elastic limit, the lateral stress maintains a constant ratio to the linear strain called Poisson's ratio.

Modulus of Elasticity Relation

Relation Between Modulus of Elasticity and Modulus of Rigidity

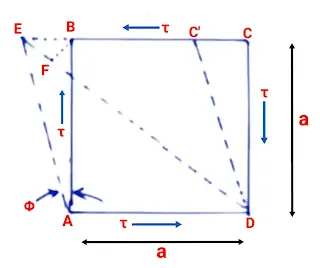
Consider a square element ABCD of sides 'a' subjected to pure shear as shown in the figure.

AEC'D is a deformed shape due to shear τ. 

Draw a perpendicular BF to diagonal DE.

Let  Φ be the shear strain and & G modulus of rigidity.

Strain in the diagonal, BD 

= (DE - DF)/DF

= EF/DB

Since,

DB² = AD² + AB²

DB = √(a² + a²)

DB = √(2a²)

DB = AB√(2)

Hence,

BD = = EF/AB√(2)

Since the angle of deformation is very small so we can assume ∠BEF = 45°

So,

cos 45 = EF/BE

EF = BE cos45

Hence,

BD = BE cos45/AB√(2)

Now, ∠ABE

tanΦ = BE/AB

BE = AB.tanΦ

BE = a.tanΦ

So,

BD = a.tanΦ.cos45/a.√(2)

BD = 1/2 . tanΦ

Since Φ is very small so tanΦ = Φ

BD = 1/2 . Φ

BD = 1/2 . τ/G  .....  ( equation 1)

As we know tensile strain along diagonal DB,

τ/E + μ.τ/E = τ/E(1 + μ) .....  ( equation 2)

From equation 1 & 2,

1/2 .τ/G  = τ/E(1 + μ)

 

After solving,

E = 2G(1 + μ)

Where,

E = Modulus of Elasticity or Young's modulus

G  = Modulus of Rigidity or Shear Modulus

μ = Poisson's Ratio

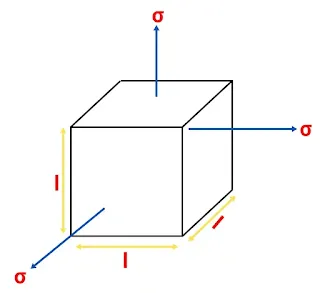
Relation Between Modulus of Elasticity and Bulk Modulus

Lets,

σ = Stress on the faces

I = length of the cube

E = Young's modulus for the Material

μ = Poisson Ratios

As we know,

Bulk Modulus, K = σ/εᵥ

Young's Modulus, E = σ/ε

Volume of cube = l³

So,

Change in Volume,

ΔV = 3l².δl

Both sides dividing by V

ΔV/V = (3l².δl)/V

ΔV/V = (3l².δl)/l³

ΔV/V = 3 × δl/l

ΔV/V = 3 × ε

As we know,

Linear strain,

ε = σ/E(1 - 2/m)

Now, putting these values then,

ΔV/V = 3 × σ/E(1 - 2/m)

Now, bulk modulus

K = σ/(ΔV/V)

K = σ/(3 × σ/E(1 - 2/m)

K = E/3(1 - 2/m)

E = 3K(1 - 2/m)

As we know,

Poisson's Ratio, μ = 1/m

So,

E = 3K(1 - 2μ)

Where,

E = Modulus of Elasticity or Young's modulus

K  = Bulk Modulus

μ = Poisson's Ratio

Relation Between Modulus of Elasticity, Bulk Modulus, and Shear Modulus

As we know from the above formula,

E = 2G(1 + μ)

So,

μ = (E/2G) - 1

Now, we know

E = 3K(1 − 2μ)

After putting Poisson's Ratio value then,

E = 3K{(1 −  2(E/2G) - 1)}

After calculating these values we will get,

E = 9KG/(3K+G)

Where,

E = Modulus of Elasticity or Young's modulus

K  = Bulk Modulus

μ = Poisson's Ratio

G  = Modulus of Rigidity or Shear Modulus

Calculation

Question.1

A 60 kg block hangs from a wire that has a cross-sectional area of 2 mm² with an applied force of 600 N. The wire was originally 4 m long but stretches by 3 cm under the load. What is Young's Modulus or modulus of elasticity of the wire?

Solution

Given Data,

M = 60 Kg

F = 600 N

A = 2 mm² = 2 × 10⁻⁶ m² 

l = 4 m

Δl = 3 cm = 3 × 10⁻² m

As we know,

E = (F × l)/(Δl × A)

Now putting the values on the above equation,

E = (600 × 4)/(3 × 10⁻² × 2 × 10⁻⁶)

E = 2400/(6 × 10⁻⁸)

E = 400 × 10⁸ N/m² or pa

Question.2

A Steel Bar 40 mm X 40 mm in section and 3 m long is subjected to an axial pull of 128 kN. If a change in length is 1.2 mm. Calculate the modulus of elasticity.

Solution

Given,

A = 40x 40 = 1600 mm² 

l = 3m = 3000 mm

P = 128 KN = 128 x 10³ N 

Δl = 1.2 mm 

E =?

As we know,

σ = F/A

So,

σ = 128 x 10³/1600 

σ = 80 N/mm² 

Now,

ε = Δl/l

So,

ε = 1.2/3000

ε = 4 × 10⁻⁴

Now, As we know

E = σ/ε

Now putting the values on the above equation

E = 80/(4 × 10⁻⁴)

E = 200 × 10³ N/mm² 

E = 200 KN

FAQ Related to Modulus of Elasticity

Why modulus of elasticity is important?

The modulus of elasticity is a measure of the stiffness of a material. It determines how much a material will deform under a given load, and is an important factor in the design of structures and mechanical components. For example, in the design of a bridge, the modulus of elasticity of the steel used in the construction of the bridge will determine how much the bridge will bend or sway under the weight of the cars and trucks that pass over it. In general, materials with a higher modulus of elasticity are stiffer and stronger and are therefore more suitable for use in structures and mechanical components that are subjected to large loads or forces.

Are Young's modulus and modulus of elasticity the same?

Yes, Young's modulus and the modulus of elasticity are the same things. Young's modulus is a measure of the stiffness of a material and is defined as the ratio of the stress applied to a material to the strain that results from the stress. It is an important property of a material and is used to predict how a material will behave under load. The modulus of elasticity is another name for Young's modulus and is often used in engineering and materials science to describe the stiffness of a material.

What is meant by the modulus of elasticity?

The modulus of elasticity measures the resistance of a material to elastically deform when a force is applied to material.  

What are the 3 modulus of elasticity?

The three modulus of elasticity is young’s modulus, shear modulus and the last bulk modulus.

What is the SI unit of Young's modulus of elasticity?

In the SI system, the unit of the modulus of elasticity is N/m² or Pascal.

So here you have to know all aspects related to the modulus of elasticity or young's modulus. If you have any doubts then you are free to ask me by mail or on the contact us page.

Thank You.