In this article, you will learn a complete overview of the polar moment of inertia such as its definition, formula, unit, derivation, application, calculation, and many more.
The polar moment of inertia is a measure of an object's ability to resist torsion, mainly cylindrical shafts.
Whereas, a simple moment of inertia is the measure of an object's ability to resist bending, mainly beams.
So, without wasting time let's get started.
What is the Polar Moment of Inertia?
The polar moment of inertia is defined as a measurement of a round bar's capacity to oppose torsion.
The polar moment of inertia is also known as the second polar moment of area.
The polar moment of inertia is the moment of inertia of a cross-section with respect to its polar axis, which is an axis at right angles to the plane of the cross-section.
For example in a rectangular rubber eraser, when torque ( load ) is applied, it undergoes torsional deformation. The section will resist this torsional deformation. This resistance against twisting is known as the polar moment of inertia.
Mathematically,
The polar moment of inertia is the moment of inertia about the third axis i.e Z - axis.
lt it is denoted by J or Iₚ.
Iₚ = Iₓ + Iᵧ
The SI unit for the polar moment of inertia is meters to the fourth power which is m⁴.
Derivation of the Polar Moment of Inertia
The moment of inertia of an area of a plane figure with respect to an axis perpendicular to the x - y plane and passing through a pole O ( z-axis ) is called the polar moment of inertia and is denoted by J, or Iₚ.
Moment of inertia of dA about z-axis = dA r²
Moment of inertia of plane area A about z - axis,
Iₚ = ∫(dA).r²
Where,
r² = x² + y²
So,
Iₚ = ∫(x² + y²)dA
Iₚ = ∫ x²dA + ∫ y²dA
Where,
Iₓ = ∫y²dA
Iᵧ = ∫x²dA
Iₚ = Iₓ + Iᵧ
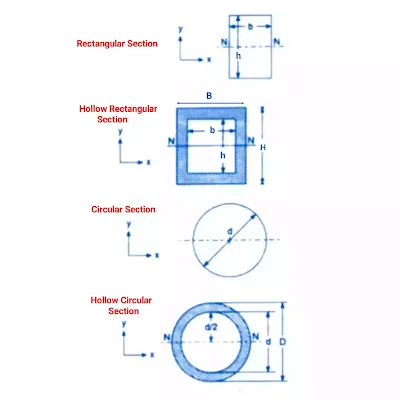
Polar Moment of Inertia for a Different Section
See in the figure the different sections whose polar moment of inertia we will discuss in detail below.
Rectangular Section
As we know,
The moment of inertia for the rectangular section about the x-axis is,
Iₓ = bh³/12
The moment of inertia for the rectangular section about the y-axis is,
Iᵧ = hb³/12
So, the polar moment of inertia for the rectangular section,
Iₚ = Iₓ + Iᵧ
Iₚ = bh³/12 + hb³/12
Iₚ = (bh/12)(bh² + hb²)
Hollow Rectangular Section
As we know,
The moment of inertia for the hollow rectangular section about the x-axis is,
Iₓ = (BH³ - bh³)/12
The moment of inertia for the hollow rectangular section about the y-axis is,
Iᵧ = (HB³ - hb³)/12
So, the polar moment of inertia for the hollow rectangular section,
Iₚ = Iₓ + Iᵧ
Circular Section
As we know,
Moment of inertia for a circular Shaft,
I = (π/64) × d⁴
So,
Iₓ = (π/64) × d⁴
Similarly,
Iᵧ = (π/64) × d⁴
So, the polar moment of inertia for the circular Shaft,
Iₚ = Iₓ + Iᵧ
Iₚ = (π/64) × d⁴ + (π/64) × d⁴
Iₚ = 2 × (π/64) × d⁴
Iₚ = (π/32) × d⁴
Hollow Circular Section
As we know,
Moment of inertia for a hollow Shaft,
I = (π/64) × (D⁴ - d⁴)
So,
Iₓ = (π/64) × (D⁴ - d⁴)
Similarly,
Iᵧ = (π/64) × (D⁴ - d⁴)
So, the polar moment of inertia for a hollow Shaft,
Iₚ = Iₓ + Iᵧ
Iₚ = (π/64) × (D⁴ - d⁴)+ (π/64) × (D⁴ - d⁴)
Iₚ = 2 × (π/64) × (D⁴ - d⁴)
Iₚ = (π/32) × (D⁴ - d⁴)
Hollow Shaft Vs Solid Shaft
Consider a Hollow Shaft & a Solid Shaft that have the same material, length, and weight.
So, the Hollow shaft has a higher polar moment of inertia than that of the solid shaft.
This is why a hollow shaft of the same mass as a solid shaft, is a better option for power transmission.
Similarly, you can find a polar moment of inertia in the other section.
Square Section
The polar moment of inertia for the square section.
Iₚ = a⁴/6
Semi Circle
The polar moment of inertia for the semi-circular section.
Iₚ = π.r⁴/4
Ellipse
The polar moment of inertia for the ellipse.
Iₚ = (1/4).π.a.b(a² + b²)
Torsional Loading of a Transmission Shaft
The angle of twist, in radians, for a solid round bar is,
Θ = T L/GJ
Where,
T = Torque
L = length
G = modulus of rigidity
J = Polar Moment of Inertia
So, the polar moment of inertia is used to calculate the angular displacement of an object which is subjected to a moment of force or torque.
Application of Polar Moment of Inertia
A polar moment of inertia is the measure of a section to resist twisting deformation about the reference axis.
The polar moment of Inertia is a quantity depending on the geometry of the body, just like the area.
This concept is used in various design problems where torsional stress is involved in the design of shafts, gears, coupling, the strength of welded joints, etc.
Calculation
Question
A circular shaft has a diameter of 80 mm. Find the polar moment of inertia for the shaft.
Solution
Given,
d = 80 mm
As we know,
The polar moment of inertia for the circular shaft is,
Iₚ = (π/32) × d⁴
So,
Iₚ = (π/32) × 80⁴
Iₚ = 0.0981 × 80⁴
Iₚ = 4018176 mm⁴
So here you have to know all aspects related to the polar moment of inertia. If you have any doubt then you are free to ask me by mail or on the contact us page.
Thank You.




0 Comments