In this article, you will learn what is the Law of Gearing with its derivatives and proof.
So without wasting time let's get started.
Law of Gearing
The common normal must always pass through the pitch point at the point of contact between a pair of teeth.
This is the fundamental condition that must be satisfied when designing profiles for the teeth of gear wheels.
This is also known as the law of gearing.
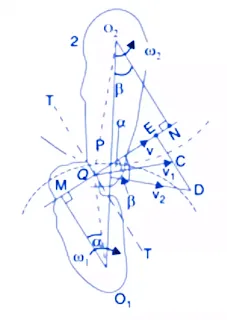
Consider the portions of the two teeth, one on wheel 1 (or pinion) and the other on wheel 2, as shown by thick line curves in Fig.
Let the two teeth come in contact at point Q, and the wheels rotate in the directions as shown in the figure.
Let TT be the common tangent and MN be the common normal to the curves at the point of contact Q.
From the centres, O1 and 02, draw O1M and O2N perpendicular to MN.
A little consideration will show that the point Q moves in the direction of QC, when considered as a point on wheel 1, and in the direction of QD when considered as a point on wheel 2.
Let V1 and V2 be the velocities of point Q on wheels 1 and 2 respectively. If the teeth are to remain in contact, the components of these velocities with the normal MN must be equal.
V1 Cosα = V2 Cosβ
(ω1 × O1Q ) Cosα = ( ω2 × O2Q )Cosβ
(ω1 × O1Q )×O1M/O1Q =( ω2 × O2Q) × O2N/O2Q
ω1 × O1M = ω2 × O2N
ω1 / ω2 = O2N/O1M
Also from similar triangles, O1MP and O2NP
O2N/O1M = O2P/O1P
So,
ω1 / ω2 = O2N/O1M = O2P/O1P
We see that the angular velocity ratio is inversely proportional to the ratio of the distance of P from the centres O1 and O2, or the common normal to the two surfaces at the point of contact Q intersects the line of centres at point P which divides the centre distance inversely as the ratio of angular velocities.
Therefore, to have a constant angular velocity ratio for all positions of the wheels, P must be the fixed point (called the pitch point) for the two wheels.
In other words, the common normal at the point of contact between a pair of teeth must always pass through the pitch point.
This is a fundamental condition that must be satisfied while designing the profiles for the teeth of gear wheels. It is also known as the law of gearing.
If Di and D2 are pitch circle diameters of wheels 1 and 2 having teeth T1 and T2 respectively, then velocity ratio,
ω1 / ω2 = O2P/O1P = D2/D1 = T2/T1
Previous Related Article:
So, I hope I've covered everything about the "law of gearing". If you still have any doubts or questions about the law of gearing, you can mail me or ask via comments, I will definitely reply to you as soon as possible.
If you liked this article then you can share it with your friends and aware of the knowledge.
Faq for Law of Gearing
Law of Gearing is Satisfied If?
The law of gearing states that common normal must always pass through the pitch point at the point of contact between a pair of teeth and the angular velocity ratio of all gears must remain constant throughout the gear mesh.
This is the fundamental condition that must be satisfied when designing profiles for the teeth of gear wheels.
Why is the Law of Gearing Followed?
The gearing law must be followed so that the two gears can transmit motion from one to the other with a constant angular velocity ratio throughout the gear mesh.
What is the Law of Gearing Formula?
The law of gearing formula can be written as
ω1 / ω2 = O2P/O1P = D2/D1 = T2/T1
Where,
ω1 = Angular velocity of gear 1.
ω2 = Angular velocity of gear 2.
D1 = Pitch circle diameter of gear 1.
D2 = Pitch circle diameter of gear 2.
T1 = Teeth of gear 1.
T2 = Teeth of gear 2.
O1P & O2P = Distance of P from the centres O1 and O2.



0 Comments