In this article, you will learn a complete overview of the parallel axis theorem such as its definition, condition, derivation, formula, and application and at the end, we will solve some numerical problems based on this theorem.
The parallel axis theorem is also called the Huygens–Steiner theorem or Steiner's theorem because it was discovered by Christiaan Huygens and Jakob Steiner.
This theorem is used to find the moment of inertia or the second moment of the area of a rigid body about any axis.
We have also discussed the perpendicular axis theorem in our previous article here we will learn only about the parallel axis theorem.
So, without wasting time let's get started.
Definition of Parallel Axis Theorem
The parallel axis theorem states that The moment of inertia of a plane section about any axis parallel to the centroidal axis is equal to the moment of inertia of the section about the centroidal axis plus the product of the area of the section and the square of the distance between the two axes.
Mathematically, It can be written as,
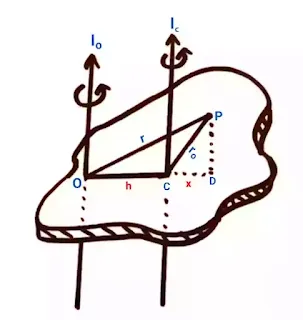
Iₒ = I꜀ + M.h²
Where,
M = Mass of the body
Iₒ = Moment of inertia about point O
I꜀= Moment of inertia of axis parallel to axis O and passing through the center of mass
Note: See the picture below
Conditions of Parallel Axis Theorem
There are the following three conditions applied to the parallel axis theorem:
- Two axes must be parallel to each other.
- One axes should pass through the center of mass.
- Always take a perpendicular distance between the two axes.
Derivation and Proof of Parallel Axis Theorem
Let,
M = Mass of the body
dm = Mass of point p
Iₒ = Moment of inertia about point O
I꜀= Moment of inertia of axis parallel to axis O and passing through the center of mass
h = Distance between two parallel axes
r = Distance between points P and O
rₒ = Distance between points P and C
As we know,
The basic formula of the moment of inertia is ∑mr².
But here we will take integration instead of summation because we have taken a small segment.
So,
Iₒ = ∫r²dm
Similarly,
I꜀ = ∫rₒ²dm
Now, △OPD applies Pythagoras theorem
OP² = PD² + OD²
Where,
OP = r
PD = (h + x)
PD = rₒ
So, after putting these values,
r² = rₒ² + (h + x)²
Since,
(a + b)² = a² + b² + 2ab
Hence,
r² = rₒ² + h² + x² + 2hx
Now multiply both sides by dm and integration
∫r² dm =∫rₒ² dm +∫h² dm +∫x² dm + ∫2hx dm
So,
Iₒ = I꜀ + ∫h² dm +∫x² dm + ∫2hx dm
Since,
∫ dm = Sum of all small masses ' dm ' which is equal to the total mass of the body M.
∫ x dm = 0, as the Algebraic sum of all moments of all particles about the center of mass is always zero when the body is in equilibrium.
So,
Iₒ = I꜀ + M.h²
Application of Parallel Axis Theorem
The common application of the parallel axis theorem is to find the moment of inertia and area moment of inertia of a given rigid body about any axis.
Below we will use the parallel axis theorem to find the moment of inertia of some body that will be away from the center.
Uniform Rod
As we know,
Moment of inertia of a rod about an axis passing through its center and perpendicular to its length
= ML²/12
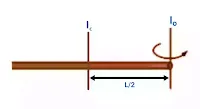
Now, we will find the moment of inertia of a rod about the axis passing through its edge.
As we know by the parallel axis theorem,
Iₒ = I꜀ + M.h²
Iₒ =(ML²/12) + M.(L/2)²
After calculating,
Iₒ = ML²/3
Ring
As we know,
M.I. of the ring about an axis passing through its center and perpendicular to the surface = MR²
M.I. of the ring about tangent and perpendicular to its plane,
Iₒ = I꜀ + M.h²
Given,
I꜀ = MR²
h = R
So,
Iₒ = MR² + MR²
Iₒ = 2 MR²
Disc
As we know,
M.I. of the disc about an axis passing through its center and perpendicular to the surface = MR²/2
M.I. of the disc about tangent and perpendicular to its plane,
Iₒ = I꜀ + M.h²
Given,
I꜀ = MR²/2
h = R
So,
Iₒ = MR²/2 + MR²
After calculating,
Iₒ = 3/2(MR²)
Sphere
Moment of inertia of a sphere around a central axis = 2/5(MR²)
Now find the moment of inertia axis through the tangent using the parallel axis theorem.
So,
Iₒ = I꜀ + M.h²
Given,
I꜀ = 2/5(MR²)
h = R
Iₒ = 2/5(MR²) + M.R²
After calculating,
Iₒ = 7/5(MR²)
Numerical of Parallel Axis Theorem
Question.1
If the moment of inertia of a body along a perpendicular axis passing through its center of gravity is 40 kg-m² and the mass of the body is 60 Kg. What is the moment of inertia of that body along another axis which is 0.3 m away from the current axis and parallel to it?
Solution:
Given Data
I꜀ = 40 Kg-m²
M = 60 Kg
h = 0.3 m
As we know, the Parallel axis theorem
Iₒ = I꜀ + M.h²
Now putting the given values
Iₒ = 40 + ( 60 × 0.3² )
Iₒ = 45.4 Kg-m²
Question.2
Calculate the moment of inertia of a rod whose mass is 50 kg and its length at the end is 0.5 m?
Solution
Given Data,
M = 50 Kg
l = 0.5 m
As we know, the parallel axis formula of a rod about the axis passes through its end.
Iₒ = ML²/3
Now putting the given values
Iₒ = (50 × 0.5²)/3
Iₒ = 12.5/3
Iₒ = 4.16 Kg-m²
FAQ Related to Parallel Axis Theorem
Why do we use a parallel axis theorem?
The parallel axis theorem is used to calculate the moment of inertia of an object when its axis of rotation is not coincident with one of the object's principal axes of inertia.
Is the parallel axis theorem always true?
The parallel axis theorem is a mathematical statement that holds true under certain conditions. These conditions are typically met when the object being considered has a symmetrical shape, such as a cylinder or a rectangular plate, and the axis of rotation is parallel to the object's principal axes of inertia.
What is the application of the parallel axis theorem?
The parallel axis theorem is used in a variety of engineering and physics applications to calculate the moment of inertia of an object about a specified axis.
So here you have to know all aspects related to the parallel axis theorem. If you have any doubts then you are free to ask me by mail or on the contact us page.
Thank You.






1 Comments