In this article, you will learn a complete overview of the area moment of inertia or second moment of area such as its definition, formula of different sections, units, calculation, and many more.
The area moment of inertia is a geometrical property of an area that indicates how its points are distributed about an axis.
It signifies the resistance of an area against the applied moment ( bending moment or twisting moment ) about an axis.
We have also discussed polar moment of inertia, and first moment of area, in our previous article here we will learn only about the area moment of inertia.
So without wasting time let's get started.
Definition of Area Moment of Inertia
The area moment of inertia is a geometrical property of an area that measures how its points are distributed with regard to an arbitrary axis, providing measures of how efficiently the cross-sectional shape can resist bending caused by loading.
The area moment of inertia is also called the second moment of inertia, second moment of area, or second area moment.
It is denoted by I.
Formula of Second Moment of Area
The first thing to note is that the area moment of inertia is not a unique property of a cross-section.
It measures the resistance to bending or twisting about a particular axis, and hence its value changes depending on where we place this reference axis.
We can estimate the area moment of inertia of a cross-section by dividing it into smaller elements shown in the figure.
Each element contributes to the total area of inertia, equal to its area dA multiplied by d².
Here d² is the distance from the reference axis.
We can sum up the values for all of the small elements to obtain the area moment of inertia for the entire cross-section.
Mathematically,
I = Σd².dA
We can more precisely define the area moment of inertia using integration like this:
I = ∫d².dA
The area moment of inertia around yy is calculated using distance to the arbitrary axis yy, given the coordinate along xx. As shown in the above figure.
Iᵧᵧ = ∫x².dA
Where,
Iᵧᵧ = Area Moment of Inertia related to the y axis
x = the perpendicular distance from axis y to the element dA
dA = An elemental area
and,
The area moment of inertia around xx is calculated using distance to the arbitrary axis xx, given the coordinate along with yy.
Iₓₓ = ∫y².dA
Where,
Iₓₓ = Area Moment of Inertia related to the x-axis
y = The perpendicular distance from axis x to the element dA
dA = An elemental area
Area Moment of Inertia of about x' and y' Axis
Sometimes it is necessary to calculate the area moment of inertia of a body with respect to the x' and y' axes.
We can calculate the moment of area for the x' and y' axes using two theorems.
- Parallel Axis Theorem
- Perpendicular Axis Theorem
Parallel Axis Theorem
The parallel axis theorem states that The moment of inertia of a plane section about any axis parallel to the centroidal axis is equal to the moment of inertia of the section about the centroidal axis plus the product of the area of the section and the square of the distance between the two axes.
Mathematically, It can be written as,
Iₓ, = Iₓ + Ad²
Where,
A = area of the body
Iₓ = Area Moment of inertia about point x
d = Perpendicular distance between the two lines x and x'.
Iₓ, = Area Moment of inertia about point x'
A similar method can be applied to calculate a moment of area about y' axis.
Perpendicular Axis Theorem
The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all three axes are mutually perpendicular and have a common point.
This theorem is also called the polar axis theorem.
Mathematically,
Iz = Iₓ + Iᵧ
Where,
Iz = Moment of Inertia about the Z axis
Iₓ = Moment of Inertia about the X axis
Iᵧ = Moment of Inertia about the Y axis
Unit of Second Moment of Inertia
In SI Unit,
As we know, the second moment of area
I = Σd².dA
So,
I = m² × m²
I = m⁴ or mm⁴
Similarly in the CGS unit, it will be,
I = cm⁴
So, The second moment of inertia has the unit of length to the fourth power.
Area Moment of Inertia for Different Shapes
Rectangular Section
As we know,
The second moment of inertia in relation to an axis:
I = ∫d².dA
So,
Area Moment of Inertia related to the y axis
Iₓₓ = ∫y².dA
Iₓₓ = ∫y².bdy = [(b.y³)/3] ( from -h/2 to h/2)
Iₓₓ = [(b.h³)/12]
Similarly,
Area Moment of Inertia related to the x-axis
Iᵧᵧ = ∫x².dA = [(h.x³)/3] ( from -b/2 to b/2 )
Iᵧᵧ = [(h.b³)/12]
Similarly,
Hollow Rectangular Section
Iₓₓ = [(B.H³)/12] - [(b.h³)/12]
Iᵧᵧ = [(H.B³)/12] - [(h.b³)/12]
Square Section
Iₓₓ = Iᵧᵧ = a⁴
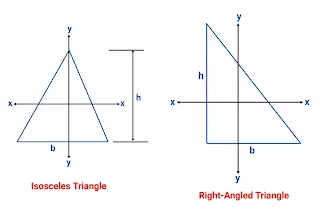
Now, Shown in the figure isosceles triangle and a right-angled triangle the second moment of Inertia is given below.
Isosceles triangle
Iₓₓ = [(b.h³)/36]
Iᵧᵧ = [(h.b³)/48]
Right-Angled Triangle
Iₓₓ = [(b.h³)/36]
Iᵧᵧ = [(h.b³)/36]
Now, show in the figure circle, semi-circle, and quarter circle that the second moment of area is calculated one by one.
Circle
Let a small element dA.
So,
dA = r.dr.dθ
y = rsinθ
Iₓₓ = ∫y².dA
= 4 ∫ ∫r²sin²θ.r.dr.dθ ( from 0 to r and 0 to π/2)
= 4 ∫r³dr ∫sin²θ.dθ
After calculating,
Iₓₓ = (πr⁴)/4 = (π/64)d⁴
So,
Iₓₓ = Iᵧᵧ = (π/64)d⁴
Similarly,
Semi Circle
Iₓₓ = Iᵧᵧ = (π/128)d⁴
Quarter Circle
Iₓₓ = Iᵧᵧ = (π/256)d⁴
Calculation of Second Moment of Area
Question
Determine the area moment of inertia about the centroidal x and y axes for the rectangular area of 600 mm height and 400 mm width.
Solution
Given Data
h = 600 mm
b = 400 mm
As we know,
The second moment of area for the rectangular section,
For x-axis,
Iₓₓ = [(b.h³)/12]
So,
Iₓₓ = [(400 × 600³)/12]
Iₓₓ = 7200 × 10⁶ mm⁴
For y-axis,
Iᵧᵧ = [(h.b³)/12]
Iᵧᵧ = [(600 × 400³)/12]
Iᵧᵧ = 3200 × 10⁶ mm⁴
FAQ Related to Area Moment of Inertia
Why is the area moment of inertia important?
The area moment of inertia is a measure of a shape's resistance to bending and torsion. It is used in the calculation of the deflection of a beam under a load and in determining the strength of a beam or shaft in relation to its ability to resist bending. It is also used in the calculation of stresses and strains in beams and other structural elements. In short, it plays a significant role in the structural analysis and design of beams, columns, and other mechanical components.
What is the area moment of inertia units?
The units of an area moment of inertia are typically expressed in terms of length to the fourth power (L⁴).
So, In the SI system, it is measured in m⁴ or mm⁴, and in the CGS system, it is measured in cm⁴.
Where,
m = meter
mm = millimeter
cm = centimeter
Why is it called the second moment of the area?
The area moment of inertia, also known as the second moment of area, is so named because it is the second moment of the area distribution about a given axis. The first moment of the area distribution is known as the first moment of the area or the centroid.
What does a higher area moment of inertia mean?
A higher area moment of inertia for a shape means that it has a greater resistance to bending or twisting. It means that the shape is stiffer and more difficult to deform.
What does the area moment of inertia depend on?
The area moment of inertia of a body depends on several factors, including the Shape of the body, Axis of the rotation, Size, and Dimensions of the body, Mass of the body, and many more.
So here you have to know all aspects related to the second moment of area or the second moment of inertia.
If you have any doubts then you are free to ask me by mail or on the contact us page.
Thank You.






0 Comments