In this article, you will learn a complete overview of the shear modulus or shear modulus of rigidity such as its definition, formula, unit, derivation, relation, calculation, and many more.
The shear modulus of rigidity or shear modulus is one of the types of elastic constant.
Elastic constants are those constants that determine the deformation produced by a given stress system acting on any material.
The elastic constant measures the elasticity of the material.
It is used to derive the relationship between stress and strain.
For a homogeneous and isotropic material, there are four types of elastic constants:
- Modulus of Elasticity or Young’s modulus
- Modulus of rigidity or Shear modulus
- Bulk modulus
- Poisson’s Ratio
Here we only discussed the shear modulus or shear modulus of rigidity.
Modulus of elasticity, bulk modulus, and poisson's ratio is already discussed in our previous article.
So before knowing shear modulus first of all we have to know about shear stress and shear strain.
So, without wasting time let's get started.
What is Shear Stress?
Shear stress is nothing but It is the resistive force that is exerted by a body per unit area of cross-section when a tangential or parallel force is applied to the body.
It is represented by the τ and its unit of
N/m² or Pascal.
What is Shear Strain?
Shear strain is the deformation of a material in response to an applied shear force.
It is measured in terms of the angle by which the material has been displaced.
Shear strain is the ratio of a relative of any layer to its perpendicular displacement distance from the fixed layer.
It is a unit less quantity and denoted by Φ.
Shear Modulus
When the material is loaded within its proportional limit under shear, the shear stress is directly proportional to the shear strain.
So within the proportional limit, the ratio of shear stress to shear strain is always constant.
This constant is known as the Shear Modulus or Modulus of Rigidity.
It is denoted by G.
Mathematically,
According to hook's law stress is proportional to strain.
When considering shear stress and shear strain then,
Shear stress is proportional to the shear strain.
So,
τ ∝ Φ
τ = G.Φ
G = τ/Φ
Where,
G = Shear modulus or modulus of rigidity
τ = Shear stress
Φ = Shear strain
It is used to calculate deformations when a deforming force acts parallel to the surface of an object.
Shear Modulus Formula
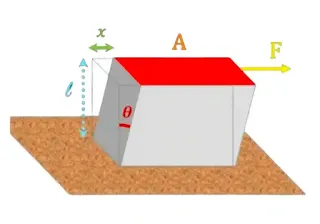
Let an object which is fixed at the bottom and a tangential force is applied to the top layer of the object then this tangential force develops shear stress in the object.
So,
Shear Stress = Tangential Force/A
Shear stress, τ = F/A
Due to this tangential force, the top of the object is deformed by changing its shape, causing the top layer of the object to be displaced by x distance.
So,
Shear Strain = Displacement of a top layer/Its distance from a fixed surface
Shear strain, Φ = x/l = tanθ
If θ is very small then,
tan θ = θ
As we know,
G = (F/A)/(x/l)
G = (F/A)/(x/l)
G = F.l/A.x
Where,
F = Tangential force
l = Distance of the object from the fixed surface to the top layer
A = Area
x = Top layer displacement of an object with respect to the bottom layer
Unit of Shear Modulus
SI Unit
As we know the unit of shear stress in the SI system is N/m² and the unit of shear strain is unit less.
So,
Shear Modulus = Shear Stress/Shear Strain
= N/m²
Hence in the SI system, the unit of the shear modulus will be N/m² or Pascal.
FPS Unit
As we know the unit of shear stress in the FPS system is lb/ft² and the unit of shear strain is unit less.
So,
Shear Modulus = Shear Stress/Shear Strain
= lb/ft²
Hence in the SI system, the unit of the shear modulus will be lb/ft².
Shear Modulus Dimensional Formula
As we know,
G = τ/Φ
Since,
Shear Stress = Force/Area
As we know,
Force = mass (m) × acceleration (a)
So,
Stress = {mass (m) × acceleration (a)}/A
As we know the unit of mass is kg, the unit of acceleration is m/s² and the unit of area is m².
So,
τ = kg × m s ⁻²/m²
τ = kg × s ⁻²/m
τ = ML⁻¹T⁻²
Since the shear strain is a unit-less quantity so the shear modulus or modulus of rigidity dimensional formula will be:
G = ML⁻¹T⁻²
Relation Between Shear Modulus and Modulus of Elasticity
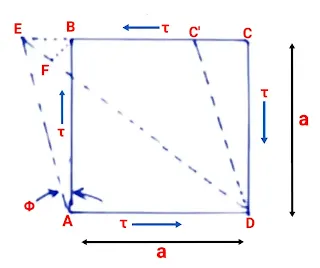
Consider a square element ABCD of sides 'a ' subjected to pure shear as shown in the figure.
AEC'D is a deformed shape due to shear τ.
Draw a perpendicular BF to diagonal DE.
Let Φ be the shear strain and & G modulus of rigidity.
Strain in the diagonal, BD
= (DE - DF)/DF
= EF/DB
Since,
DB² = AD² + AB²
DB = √(a² + a²)
DB = √(2a²)
DB = AB√(2)
Hence,
BD = = EF/AB√(2)
Since the angle of deformation is very small so we can assume ∠BEF = 45°
So,
cos 45 = EF/BE
EF = BE cos45
Hence,
BD = BE cos45/AB√(2)
Now, ∠ABE
tanΦ = BE/AB
BE = AB.tanΦ
BE = a.tanΦ
So,
BD = a.tanΦ.cos45/a.√(2)
BD = 1/2 . tanΦ
Since Φ is very small so tanΦ = Φ
BD = 1/2 . Φ
BD = 1/2 . τ/G ..... ( equation 1)
As we know tensile strain along diagonal DB,
τ/E + μ.τ/E = τ/E(1 + μ) ..... ( equation 2)
From equation 1 & 2,
1/2 .τ/G = τ/E(1 + μ)
After solving,
E = 2G(1 + μ)
Relation Between Shear Modulus, Bulk Modulus, and Modulus of Elasticity
As we know from the relation between the modulus of elasticity and shear modulus,
E = 2G(1 + μ)
So,
μ = (E/2G) - 1
Now, we know
E = 3K(1 − 2μ)
After putting Poisson's Ratio value then,
E = 3K{(1 − 2(E/2G) - 1)}
After calculating these values we will get,
E = 9KG/(3K+G)
Calculation
Question
Material has a young's modulus of 2×10⁵ N/mm² and Poisson's ratio of 0.32. Calculate the modulus of rigidity or shear modulus.
Solution
Given,
E = 2×10⁵ N/mm²
μ = 0.32
G =?
We know that,
E = 2G(1 + μ)
2×10⁵ = 2G(1 + 0.32)
After solving
G = 75.75 × 10³ N/mm²
FAQ Related to Shear Modulus
What does a higher shear modulus mean?
The shear modulus is a measure of a material's resistance to shear stress. It is defined as the ratio of shear stress to shear strain in the material.
A higher shear modulus means that the material is more resistant to shear stress and will deform less under the same amount of shear strain.
For example, a material with a high shear modulus will be more difficult to deform when subjected to a shear force, such as when two opposing surfaces of the material are pushed or pulled in opposite directions. Conversely, a material with a low shear modulus will be more easily deformed under shear stress.
What is the shear modulus of steel?
The shear modulus of steel can vary depending on the specific type of steel and its microstructure. In general, the shear modulus of steel is in the range of 80 to 200 gigapascals (GPa).
For example, the shear modulus of carbon steel at room temperature is typically around 80 GPa.
This value can increase slightly with temperature and decrease at very low temperatures due to the material's change in the crystal structure. The shear modulus of stainless steel is generally slightly higher than that of carbon steel, in the range of 90 to 120 GPa.
What is shear modulus measured in?
The shear modulus is typically measured in units of pressure, such as pascals (Pa), megapascals (MPa), or gigapascals (GPa).
The shear modulus is defined as the ratio of shear stress to shear strain in a material and is typically expressed in units of pressure because shear stress is typically measured in units of pressure.
What is the relation between shear modulus and elastic modulus?
The relation between shear modulus and elastic modulus can be formulated by E = 2G(1 + μ).
So here you have to know all aspects related to the shear modulus of rigidity or shear modulus.
If you have any doubts then you are free to ask me by mail or on the contact us page.
Thank You.



0 Comments