Hello friends Today, we will learn about types of pattern allowances which is used in the casting process.
Before knowing the types of pattern allowances firstly we have to know what is a pattern and where to use it?
So, without wasting time let's get started.
What is Pattern?
For making the casting product in the casting process, a pattern is used to make a mold cavity in the sand.
A pattern is similar to the casting product but not exactly the same size, given some allowance because of the shrinkage property of cast metal.
The pattern materials can be made of wood, metal, plastic, compound, or wax.
Usually, the patterns are made of wood only because they are cheap, and they are also easy to make.
Pattern Allowance
A pattern is a replica of casting which is used to make a mold cavity but it has slightly large dimensions.
This change in the pattern is due to when the cast solidifies, it shrinks at some limit due to metal shrinkage property at the time of cooling.
So to compensate for this, a pattern is made a little bigger.
These slight changes in the pattern are known as pattern allowance.
Types of Pattern Allowance
There are the following types of pattern allowances are used in the casting process.
- Shrinkage Allowance
- Draft Allowance
- Machining Allowance
- Deformation or Camber Allowance
- Shake or Rapping Allowance
Shrinkage Allowance
Shrinkage is defined as the reduction during the cooling or solidification process.
This is a common property of all materials.
The magnitude of shrinkage varies from material to material, but each and every material has to shrinks.
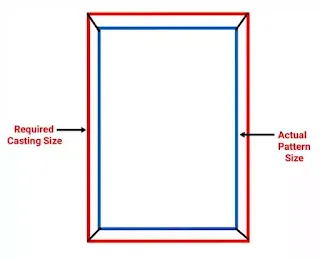
For avoiding this, the pattern is made larger than the required size of the casting product with the help of the shrink rule.
Then the difference between actual pattern size and required casting size is known as shrinkage allowance.
Show in the figure.
The shrinkage allowance is given in the pattern in mm/m (millimeter/meter).
Which is different for different materials.
Shrinkage Allowances For Different Materials
There are following some shrinkage allowance given inside the pattern for different materials are used in casting.
- For grey cast iron shrinkage allowance is given from 6.95 to 10.5mm/m.
- For white cast iron and steel, it is given up to 20.8 mm/m.
- For Aluminium shrinkage allowance given 17 mm/m and for aluminum alloy given from 12.5 to 15 mm/m
- For brass, it is given up to 15.3 mm/m.
Types of Shrinkage
There are following three types of shrinkage that happen during the casting process.
- Liquid Shrinkage
- Solidification Shrinkage.
- Solid Shrinkage
Liquid Shrinkage
The liquid contraction that occurs during cooling before solidification is called liquid shrinkage.
After pouring the molten metal into the mold cavity, the level of the molten metal decreases during cooling due to the liquid shrinkage.
Solidification Shrinkage
The contraction phase changes from liquid to solid, which is called solidification shrinkage.
The solidification shrinkage reduces the height of the casting metal.
Solid Shrinkage
The shrinkage of solidified casting at room temperature due to thermal contraction is called solid shrinkage.
The solid shrinkage further reduces the height of the casting metal.
Draft Allowance
During removing the pattern from the mold cavity, the parallel surfaces in the direction in which the pattern is withdrawn are slightly damaged and also converted into slightly tapered surfaces.
To compensate for these changes, these parallel surfaces on the pattern are slightly tapered by about 1 to 2 degrees.
By which removal of the pattern from the mold cavity becomes easy and suitable and also does not affect the casting in any way.
These small changes in the surface of the pattern are called draft allowances to protect it from damage.
See in the figure.
Machining Allowance
As we know that the product of the casting process gives a very poor surface finish, so the surface of the final product of casting always is rough.
But we required a product that is polished and has a good surface finish.
So in order to have a good surface finish, the final product of the casting is machined with the help of a lathe machine, milling machine, shaper machine, slotting machine with these processes such as turning, grinding, shaping, drilling to obtain a surface finish.
This allowance is added to the basic size of the pattern.
It ranges from less than 2 mm to 15 mm depending on the size and material of the pattern.
Show in the figure casting product before machining with allowances and after machining.
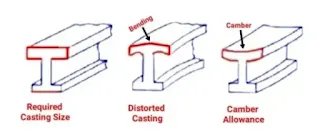
Deformation or Camber Allowance
When the metal is in the cooling process, stress is developed during the solidifying of this metal due to uneven metal thickness in the casting process.
This stress can cause deformation or bend in the casting.
To avoid this bending or deformation in castings, camber is provided in the opposite direction so that when bending occurs due to uneven thickness of metal, the casting product becomes straight.
These small changes in a pattern to avoid bending in the casting process are called bending or camber allowances.
Show in the figure camber provided in a pattern.
Shake or Rapping Allowance
When the pattern is to be removed from the sand of the casting, a slight shake is required to remove the pattern from the sand and this will increase the dimension of the casting slightly.
To avoid this increase in the dimension of the casting, the pattern is made slightly smaller than the casting.
These small changes in the dimensions of the pattern in the casting process are called the shaking or rapping allowance.
See in a figure shaking or rapping allowance.
In this post, we’ve to know the types of pattern allowances and their uses.
So friends I hope you all like this post.
Thank You.
FAQ Related to Pattern Allowances
Which pattern allowance is Negative allowance?
Shake or rapping pattern allowance is known as the negative allowance.
Why is pattern allowance required?
Due to shrinkage property of cast metal pattern allowances given to the pattern in casting process.
How many types of allowances are there in casting?
Pattern allowances are five types shrinkage, draft, machining, deformation and rapping allowances.
To have good surface finish and accuracy which of the allowance is given?
For good surface finish and accuracy machining allowance is given.
Which types of pattern allowances used to reduce the chances of damage due to withdrawing of a pattern from the mould cavity?
Draft allowances used to reduce the chances of damage during withdrawing of a pattern from the mould cavity.






6 Comments